Estom的博客

n个骰子的点数 生成幂集的循环方法。完全一致，也是动态规划问题。 1 n个骰子的点数问题描述 把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。你需要用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。 示例 1: 123456输入: 1输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]示例 2:输入: 2输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778] 问题分析策略选择算法设计 使用动态规划解决问题一般分为三步： 确定状态变量 确定状态转移方程 边界处理 表示状态 分析问题的状态时，不要分析整体，只分析最后一个阶段即可！因为动态规划问题都是划分为多个阶段的，各个阶段的状态表示都是一样，而我们的最终答案在就是在最后一个阶段。 通过题目我们知道一共投掷 n 枚骰子，那最后一个阶...

作业调度问题 参考文献 https://zhuanlan.zhihu.com/p/30705914 问题描述有n个作业需要在2台机器M1 和M2组成的流水线上完成加工。每个作业都必须先在 M1 上加工，然后在 M2 上加工。M1和M2加工作业i所需的时间分别记作 a_i和b_i，每台机器同一时间最多只能执行一个作业。 请确定这n个作业的最优加工顺序，使得从第一个作业在机器上开始加工，到最后一个作业在机器上加工完成所需的时间最少。 问题分析算法设计 johnson不等式。满足min{bi,aj}>= min{bj,ai}则表示i和j满足johnson不等式。则意味着i在j前执行，不会使的结果变坏。 查参考文献。 算法分析 时间复杂度O(nlogn)按json不等式排序的时间复杂度。 算法实现

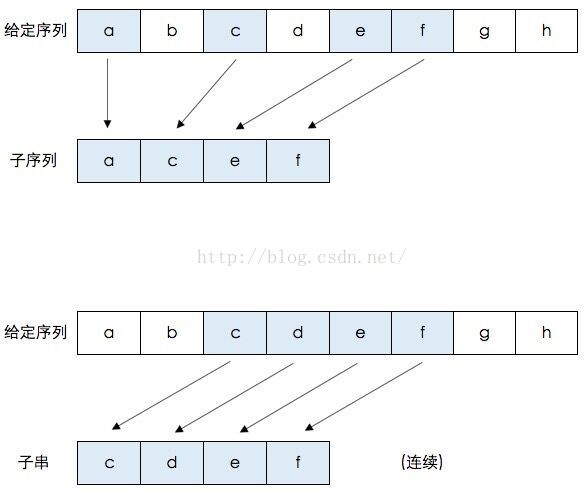
最长公共子序列问题描述求数组A和B的最长公共子序列 问题分析 子序列(subsequence)： 一个特定序列的子序列就是将给定序列中零个或多个元素去掉后得到的结果(不改变元素间相对次序)。例如序列<A,B,C,B,D,A,B>的子序列有：<A,B>、<B,C,A>、<A,B,C,D,A>等。 公共子序列(common subsequence)： 给定序列X和Y，序列Z是X的子序列，也是Y的子序列，则Z是X和Y的公共子序列。例如X=[A,B,C,B,D,A,B]，Y=[B,D,C,A,B,A[，那么序列Z=[B,C,A]为X和Y的公共子序列，其长度为3。但Z不是X和Y的最长公共子序列，而序列[B,C,B,A]和[B,D,A,B]也均为X和Y的最长公共子序列，长度为4，而X和Y不存在长度大于等于5的公共子序列。对于序列[A,B,C]和序列[E,F,G]的公共子序列只有空序列[]。 最长公共子序列：给定序列X和Y，从它们的所有公共子序列中选出长度最长的那一个或几个。 子串： 将一个序列从最前或最后或同时删掉...

投资问题问题描述m元钱，n个项目。f_i(x)表示x元钱投入项目i的效益。求最大效益。 问题分析算法设计 问题分解划分阶段：规模增长的方向有两个。第一个是投资的金额想，第二个是项目选择k。x,k阶段。 确定状态变量dp[x][k]表示投资x，第k个项目的最大收益。 确定状态转移方程。 状态转移过程。 算法效率 O(n*m^2) 算法实现

随机化算法随机算法的概述 将算法必须对所有可能的输入都正确地求解问题的条件放宽，只要求它的可能不正确性解能够相对安全地忽略掉，比如说它的出现可能性非常低;而且也不要求对于特定的输入，算法的每一次运行的输出都必须相同。 随机算法可以做如下定义：它是在接收输入的同时，为了随机选择的目的，还接收一串随机比特流并且在运行过程中使用该比特流的算法。 一个随机算法在不同的运行中对于相同的输入可以有不同的结果。由此得出对于相同的输入两次不同的随机算法的执行时间可能不同。 随机算法的优点 首先，较之那些我们所知的解决同一问题最好的确定性算法，随机算法所需的运行时间或空间通常常小一些； 其次，观察迄今为止已经发明的各种随机算法，我们发现这些算法总是易于理解和实现。 1 伪随机数伪随机数的产生$$\begin{cases} a_0=d\ a_n=(ba_{n-1}+c) mod m\end{cases}$$ 其中$a\geq 0,b\geq0,d\geq m,d$是随机序列种子。 2 数值随机化算法3 舍伍德算法 确定性算法随机化。 4 蒙特卡洛算法 蒙特...