背包问题
1 01 背包问题
问题描述
有N个物品,它们有各自的体积和价值,现有给定容量的背包c,如何让背包里装入的物品具有最大的价值总和?
N=4
i 1,2,3,4
w 2,3,4,5
v 3,4,5,6
c=8
问题分析
策略选择
算法设计
有两种动态规划的思路,本质上是一致的。背包的容量增长作为第一维,或者物品的数量增长作为第一维。
- 当背包的容量作为第一维的时候。背包容量为行,物品增长为列。
- 问题分解划分阶段。背包容量容量为i,物品选择为j
- 确定状态dp[i][j]表示背包容量为i的情况下,第j个物品放入或者不放入的最大价值。
- 确定状态转移方程。分两种情况讨论。当背包容量为i时,第j个物品放入和第j个物品不放入。
$$
dp[i][j]=max(dp[i][j-1],dp[i-w[i]][j-1])
$$
- 当物品的增长作为第一维的时候。物品增长为行,背包容量为列
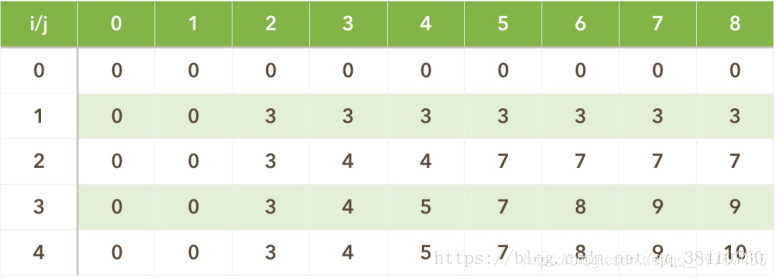
- 问题分解划分阶段:2个规模增长方向。背包的容量和物品。物品选择i。背包的容量表示为j。第一个阶段表示是否添加物品。第二个阶段是背包容量的增长。
- 确定状态dp[i][j]表示第i个物品,在背包容量j的情况下的最大价值。
- 确定状态转移方程
$$
dp[i][j]=max(dp[i-1][j],v[i]+dp[i-1][j-w[i]])
$$
两种计算方式完全一致。
算法分析
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include<iostream>
using namespace std;
#include <algorithm>
int main()
{
int w[5] = { 0 , 2 , 3 , 4 , 5 };
int v[5] = { 0 , 3 , 4 , 5 , 6 };
int bagV = 8;
int dp[5][9] = { { 0 } };
for (int i = 1; i <= 4; i++) {
for (int j = 1; j <= bagV; j++) {
if (j < w[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 9; j++) {
cout << dp[i][j] << ' ';
}
cout << endl;
}
return 0;
}
|
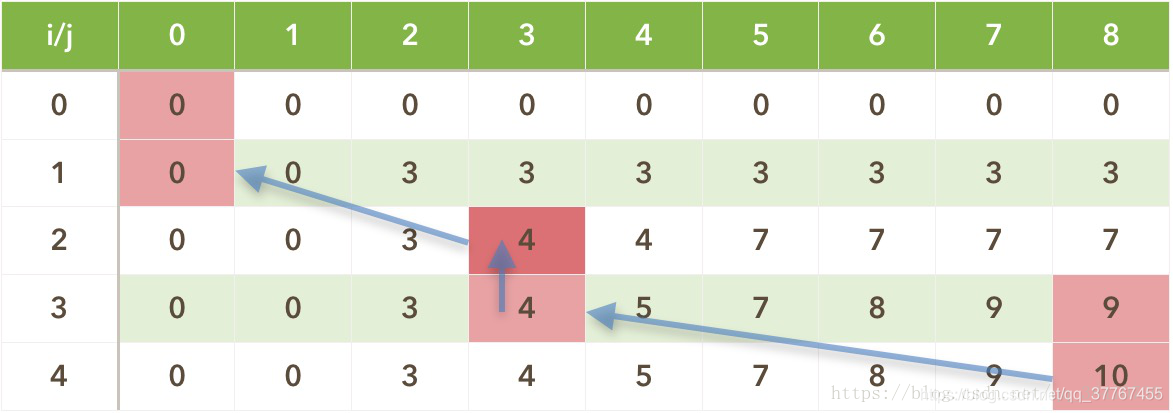
最优的背包价值路径回溯方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include<iostream>
using namespace std;
#include <algorithm>
int w[5] = { 0 , 2 , 3 , 4 , 5 };
int v[5] = { 0 , 3 , 4 , 5 , 6 };
int bagV = 8;
int dp[5][9] = { { 0 } };
int item[5];
void findMax() {
for (int i = 1; i <= 4; i++) {
for (int j = 1; j <= bagV; j++) {
if (j < w[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
}
void findWhat(int i, int j) {
if (i >= 0) {
if (dp[i][j] == dp[i - 1][j]) {
item[i] = 0;
findWhat(i - 1, j);
}
else if (j - w[i] >= 0 && dp[i][j] == dp[i - 1][j - w[i]] + v[i]) {
item[i] = 1;
findWhat(i - 1, j - w[i]);
}
}
}
void print() {
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 9; j++) {
cout << dp[i][j] << ' ';
}
cout << endl;
}
cout << endl;
for (int i = 0; i < 5; i++)
cout << item[i] << ' ';
cout << endl;
}
int main()
{
findMax();
findWhat(4, 8);
print();
return 0;
}
|
2 完全背包问题
问题描述
完全背包(unbounded knapsack problem)与01背包不同就是每种物品可以有无限多个:一共有N种物品,每种物品有无限多个,第i(i从1开始)种物品的重量为w[i],价值为v[i]。在总重量不超过背包承载上限W的情况下,能够装入背包的最大价值是多少?
问题分析
策略选择
算法设计
- 问题分解划分阶段:2个规模增长方向。背包的容量和物品。背包的个数增长i=1,2,3,n。背包容量为j。第一个阶段表示是否添加物品。第二个阶段是背包容量的增长。
- 确定状态dp[i,j]
- 确定状态转移方程
$$
dp[i][j] = max{(dp[i-1][j − kw[i]] + kv[i]) for every k}
$$
算法分析
算法实现
3 多重背包
问题描述
多重背包(bounded knapsack problem)与前面不同就是每种物品是有限个:一共有N种物品,第i(i从1开始)种物品的数量为n[i],重量为w[i],价值为v[i]。在总重量不超过背包承载上限W的情况下,能够装入背包的最大价值是多少?
算法设计
1
| dp[i][j] = max{(dp[i-1][j − k*w[i]] + k*v[i]) for every k}
|






