树状数组Binary Tree Array

1 概念

lowbit运算

$$
lowbit(x) = x & ((\sim x)+1)
$$

  • 作用：二进制表示中，保留最后的1。如x=10100100,lowbit(x)=00000100

树状数组

  • 根据lowbit的运算规则构建树状数组。
  • 其中数组A第i个位置的值管理区间[i-lowbit(i)+1,i]。即去掉二进制最后一位后到当前位置的的区间。

$$
A[i] = \sum_{k=i-lowbit(i)+1}^i A[k]
$$

  • 其中数组A第i个位置的值的被管节点。即找到所有的之后的$2^i$的点，也包括非$2^i$的点。

$$
i = i + lowbit(i) ,i<max(i)
$$

本质理解

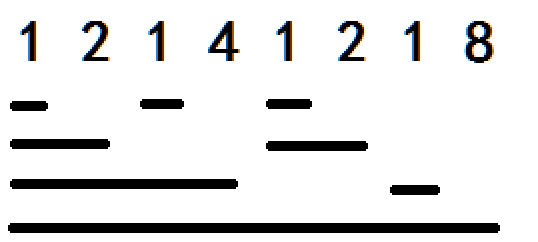
  • 怎么看每个原始数组的数字管理多少？只要顺着原始数组的数字往下画竖线，碰到的第一根横线所覆盖的范围就是它能管理的范围。

  • 怎么看每个原始数组的数字被谁管理？顺着原始数组的数字往下画竖线，碰到的第一根横线之后的所有横先，都是管理该数字的树状数组值。

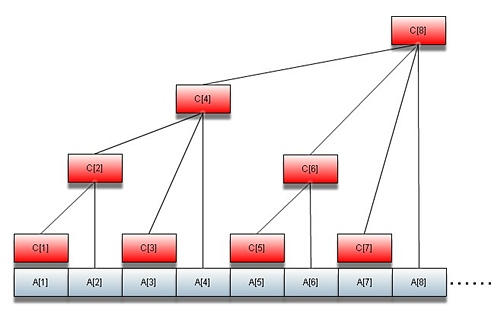
  • 在构建的树状数组中$2^i$管理之前所有位置的原始数组。即前i项和。

  • 通过lowbit()运算，构建的树状数组，本质上是一种辅助数组。

2 性质

  • 任何一个数字管理

$$
(i-lowbit(i),i]
$$

  • 任何一个数字被管理

$$
[i,i+lowbit(i)],进行迭代i=i+lowbit(i)
$$

管理的继承性：即一个数字x如果管理y，那么也一定管理了被y管理的数字。

3 应用

把位置k的元素加x

  • 我们每次执行操作A（把位置k的值+x），只需要把”能管理到k的所有位置”都+x就行
    1. i=k
    2. A[i]+x
    3. i=i+lowbit(i)
    4. 重复2-3步骤，直到i>max截止

求前缀区间的值

所有lowbit()对应的值相加。

  • 那么对于任意的x，sum(1,x)怎么求呢？我们把最终得到的答案存在ans变量中，执行下面的操作:
    1. sum=0
    2. sum += A[i]
    3. i = i-lowbit(i)
    4. 重复2-3步骤，直到i<0截止

求区间的值

  • 询问区间[L,R]的和sum(L,R)。我们只需要求出sum(1,R)和sum(1,L-1),然后sum(1,R)-sum(1,L-1)就是sum(L,R).
    $$
    sum(L,R)=sum(1,R)-sum(1,L)
    $$

创建树状数组

  • 将树状数组初始化为0.依次添加位置k的元素添加x。创建数组的时间复杂度为O(nlog n)

实例1 基本运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//求最小幂2^k:
int Lowbit(int t)
{
    return t & ( t ^ ( t - 1 ) );//把最后一个1变为0，然后再按位与。
    //return t&(-t)
    //return t&(~t+1)
}

// 创建树状数组

int tree_array(){
    for(int i=1;i<)
}

//求前n项和：
int Sum(int end)
{
    int sum = 0;
    while(end > 0)
    {
        sum += in[end];
        end -= Lowbit(end);
    }
    return sum;
}

//对某个元素进行加法操作
void plus(int pos , int num)
{
    while(pos <= n)
    {
          in[pos] += num;
          pos += Lowbit(pos);
    }
}