第五章模型后处理

作者：Trent Hauck

译者：飞龙

协议：CC BY-NC-SA 4.0

5.1 K-fold 交叉验证

这个秘籍中，我们会创建交叉验证，它可能是最重要的模型后处理验证练习。我们会在这个秘籍中讨论 k-fold 交叉验证。有几种交叉验证的种类，每个都有不同的随机化模式。K-fold 可能是一种最熟知的随机化模式。

准备

我们会创建一些数据集，之后在不同的在不同的折叠上面训练分类器。值得注意的是，如果你可以保留一部分数据，那是最好的。例如，我们拥有N = 1000的数据集，如果我们保留 200 个数据点，之后使用其他 800 个数据点之间的交叉验证，来判断最佳参数。

工作原理

首先，我们会创建一些伪造数据，之后测试参数，最后，我们会看看结果数据集的大小。

>>> N = 1000  
>>> holdout = 200
>>> from sklearn.datasets import make_regression 
>>> X, y = make_regression(1000, shuffle=True)

既然我们拥有了数据，让我们保留 200 个点，之后处理折叠模式。

1
2
3

>>> X_h, y_h = X[:holdout], y[:holdout] 
>>> X_t, y_t = X[holdout:], y[holdout:]
>>> from sklearn.cross_validation import KFold

K-fold 给了我们一些选项，来选择我们想要多少个折叠，是否让值为下标或者布尔值，是否打算打乱数据集，最后是随机状态（主要出于再现性）。下标实际上会在之后的版本中溢出。假设它为True。

让我们创建交叉验证对象：

1	>>> kfold = KFold(len(y_t), n_folds=4)

现在，我们可以迭代 k-fold 对象：

>>> output_string = "Fold: {}, N_train: {}, N_test: {}"

>>> for i, (train, test) in enumerate(kfold):
        print output_string.format(i, len(y_t[train]), len(y_t[test]))
        
Fold: 0, N_train: 600, N_test: 200 
Fold: 1, N_train: 600, N_test: 200 
Fold: 2, N_train: 600, N_test: 200 
Fold: 3, N_train: 600, N_test: 200

每个迭代都应该返回相同的分割大小。

工作原理

可能很清楚，但是 k-fold 的原理是迭代折叠，并保留 1/n_folds * N个数据，其中N是我们的len(y_t)。

从 Python 的角度看，交叉验证对象拥有一个迭代器，可以通过in运算符来访问。通常，对于编写交叉验证对象的包装器来说比较实用，它会迭代数据的子集。例如我们可能拥有一个数据集，它拥有数据点的重复度量，或者我们可能拥有一个病人的数据集，每个病人都拥有度量。

我们打算将它们组合起来，并对其使用 Pandas。

>>> import numpy as np 
>>> import pandas as pd

>>> patients = np.repeat(np.arange(0, 100, dtype=np.int8), 8)

>>> measurements = pd.DataFrame({'patient_id': patients,
                   'ys': np.random.normal(0, 1, 800)})

既然我们拥有了数据，我们仅仅打算保留特定的顾客，而不是数据点。

>>> custids = np.unique(measurements.patient_id) 
>>> customer_kfold = KFold(custids.size, n_folds=4)

>>> output_string = "Fold: {}, N_train: {}, N_test: {}"

>>> for i, (train, test) in enumerate(customer_kfold):
        train_cust_ids = custids[train]
        training = measurements[measurements.patient_id.isin(
                   train_cust_ids)]
        testing = measurements[~measurements.patient_id.isin(
                   train_cust_ids)]

        print output_string.format(i, len(training), len(testing))

Fold: 0, N_train: 600, N_test: 200 
Fold: 1, N_train: 600, N_test: 200 
Fold: 2, N_train: 600, N_test: 200 
Fold: 3, N_train: 600, N_test: 200

5.2 自动化交叉验证

我们会查看如何使用 Sklearn 自带的交叉验证，但是我们也可以使用一个辅助函数，来自动化执行交叉验证。这类似于 Sklearn 中其它对象，如何被辅助函数和流水线包装。

准备

首先，我们需要创建样例分类器，它可以是任何东西，决策树、随机森林，以及其他。对我们来说，它是随机森林。我们之后会创建数据集，并使用交叉验证函数。

工作原理

首先导入ensemble 模块来开始：

1 2	>>> from sklearn import ensemble >>> rf = ensemble.RandomForestRegressor(max_features='auto')

好的，所以现在，让我们创建一些回归数据：

1 2	>>> from sklearn import datasets >>> X, y = datasets.make_regression(10000, 10)

既然我们拥有了数据，我们可以导入cross_validation模块，并获取我们将要使用的函数：

>>> from sklearn import cross_validation

>>> scores = cross_validation.cross_val_score(rf, X, y)

>>> print scores
[ 0.86823874  0.86763225  0.86986129]

工作原理

很大程度上，它会委托给交叉验证对象。一个不错的事情是，函数会并行处理交叉验证。

我们可开启详细模式：

>>> scores = cross_validation.cross_val_score(rf, X, y, verbose=3,
             cv=4)
             
[CV] no parameters to be set 
[CV] no parameters to be set, score=0.872866 -   0.7s 
[CV] no parameters to be set 
[CV] no parameters to be set, score=0.873679 -   0.6s 
[CV] no parameters to be set 
[CV] no parameters to be set, score=0.878018 -   0.7s 
[CV] no parameters to be set 
[CV] no parameters to be set, score=0.871598 -   0.6s

[Parallel(n_jobs=1)]: Done   1 jobs       | elapsed:    0.7s 
[Parallel(n_jobs=1)]: Done   4 out of   4 | elapsed:    2.6s finished

我们可以看到，在每次迭代中，我们都调用函数来获得得分。我们也知道了模型如何运行。

同样值得了解是的，我们可以对我们尝试拟合的模型，获取预测得分。我们也会讨论如何创建你自己的评分函数。

5.3 使用 ShuffleSplit 交叉验证

ShuffleSplit是最简单的交叉验证技巧之一。这个交叉验证技巧只是将数据的样本用于指定的迭代数量。

准备

ShuffleSplit是另一个简单的交叉验证技巧。我们会指定数据集中的总元素，并且它会考虑剩余部分。我们会浏览一个例子，估计单变量数据集的均值。这有点类似于重采样，但是它说明了一个原因，为什么我们在展示交叉验证的时候使用交叉验证。

操作步骤

首先，我们需要创建数据集。我们使用 NumPy 来创建数据集，其中我们知道底层的均值。我们会对半个数据集采样，来估计均值，并看看它和底层的均值有多接近。

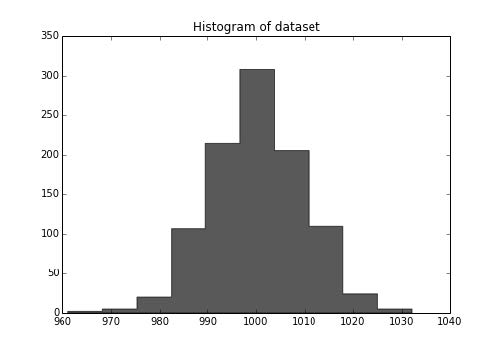
>>> import numpy as np

>>> true_loc = 1000 
>>> true_scale = 10 
>>> N = 1000

>>> dataset = np.random.normal(true_loc, true_scale, N)

>>> import matplotlib.pyplot as plt

>>> f, ax = plt.subplots(figsize=(7, 5))

>>> ax.hist(dataset, color='k', alpha=.65, histtype='stepfilled'); 
>>> ax.set_title("Histogram of dataset");

>>> f.savefig("978-1-78398-948-5_06_06.png")

NumPy 输出如下：

现在，让我们截取前一半数据集，并猜测均值：

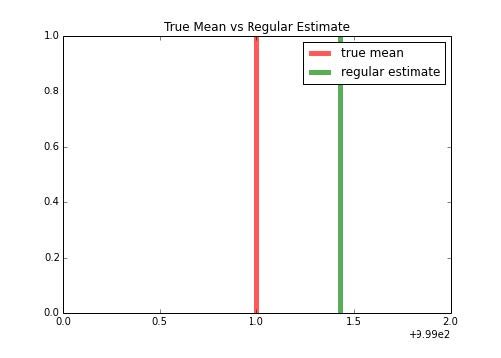
>>> from sklearn import cross_validation

>>> holdout_set = dataset[:500] 
>>> fitting_set = dataset[500:]

>>> estimate = fitting_set[:N/2].mean()

>>> import matplotlib.pyplot as plt

>>> f, ax = plt.subplots(figsize=(7, 5))

>>> ax.set_title("True Mean vs Regular Estimate")

>>> ax.vlines(true_loc, 0, 1, color='r', linestyles='-', lw=5,
              alpha=.65, label='true mean') 
>>> ax.vlines(estimate, 0, 1, color='g', linestyles='-', lw=5,
              alpha=.65, label='regular estimate')

>>> ax.set_xlim(999, 1001)

>>> ax.legend()

>>> f.savefig("978-1-78398-948-5_06_07.png")

输出如下：

现在，我们可以使用ShuffleSplit 在多个相似的数据集上拟合估计值。


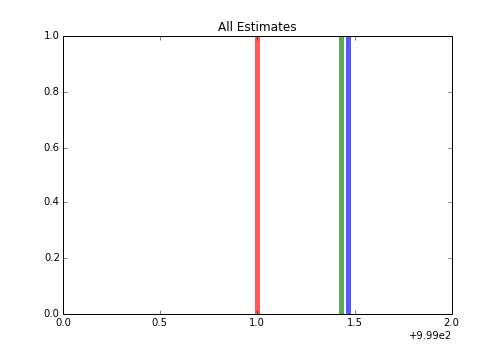
>>> from sklearn.cross_validation import ShuffleSplit

>>> shuffle_split = ShuffleSplit(len(fitting_set))

>>> mean_p = []

>>> for train, _ in shuffle_split:
        mean_p.append(fitting_set[train].mean())
        shuf_estimate = np.mean(mean_p)

>>> import matplotlib.pyplot as plt

>>> f, ax = plt.subplots(figsize=(7, 5))

>>> ax.vlines(true_loc, 0, 1, color='r', linestyles='-', lw=5,
              alpha=.65, label='true mean') 
>>> ax.vlines(estimate, 0, 1, color='g', linestyles='-', lw=5,
              alpha=.65, label='regular estimate') 
>>> ax.vlines(shuf_estimate, 0, 1, color='b', linestyles='-', lw=5,
              alpha=.65, label='shufflesplit estimate')

>>> ax.set_title("All Estimates") 
>>> ax.set_xlim(999, 1001)

>>> ax.legend(loc=3)

输出如下：

我们可以看到，我们得到了类似于预期的估计值，但是我们可能使用多个样本来获取该值。

5.4 分层的 k-fold

这个秘籍中，我们会快速查看分层的 k-fold 估值。我们会浏览不同的秘籍，其中分类的表示在某种程度上是不平衡的。分层的 k-fold 非常不错，因为他的模式特地为维持分类的比例而设计。

准备

我们打算创建一个小型的数据集。这个数据集中，我们随后会使用分层的 k-fold 验证。我们想让它尽可能小，以便我们查看变化。对于更大的样本，可能并不是特别好。

我们之后会绘制每一步的分类比例，来展示如何维护分类比例。

>>> from sklearn import datasets 
>>> X, y = datasets.make_classification(n_samples=int(1e3),
           weights=[1./11])

让我们检查分类的总体权重分布：

1 2	>>> y.mean() 0.90300000000000002

90.5% 的样本都是 1，其余为 0。

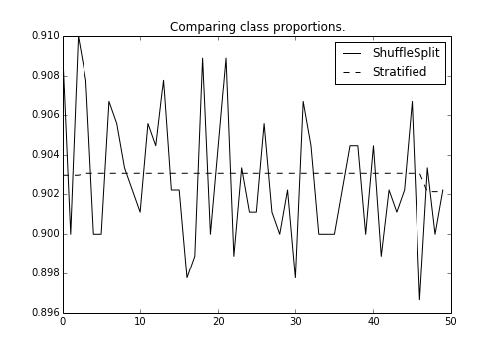
操作步骤

让我们创建分层 k-fold 对象，并通过每个折叠来迭代。我们会度量为 1 的verse 比例。之后，我们会通过分割数字来绘制分类比例，来看看是否以及如何发生变化。这个代码展示了为什么它非常好。我们也会对基本的ShuffleSplit绘制这个代码。

>>> from sklearn import cross_validation

>>> n_folds = 50

>>> strat_kfold = cross_validation.StratifiedKFold(y,
                  n_folds=n_folds) 
>>> shuff_split = cross_validation.ShuffleSplit(n=len(y),
                  n_iter=n_folds)

>>> kfold_y_props = [] 
>>> shuff_y_props = []

>>> for (k_train, k_test), (s_train, s_test) in zip(strat_kfold,  
>>> shuff_split):         
        kfold_y_props.append(y[k_train].mean())       
        shuff_y_props.append(y[s_train].mean())

现在，让我们绘制每个折叠上的比例：


>>> import matplotlib.pyplot as plt

>>> f, ax = plt.subplots(figsize=(7, 5))

>>> ax.plot(range(n_folds), shuff_y_props, label="ShuffleSplit",
            color='k') 
>>> ax.plot(range(n_folds), kfold_y_props, label="Stratified",
            color='k', ls='--') 
>>> ax.set_title("Comparing class proportions.")

>>> ax.legend(loc='best')

输出如下：

我们可以看到，分层的 k-fold 的每个折叠的比例，在每个折叠之间是稳定的。

工作原理

分层 k-fold 的原理是选取y值。首先，获取所有分类的比例，之后将训练集和测试集按比例划分。这可以推广到多个标签：


>>> import numpy as np

>>> three_classes = np.random.choice([1,2,3], p=[.1, .4, .5],
                    size=1000)

>>> import itertools as it

>>> for train, test in cross_validation.StratifiedKFold(three_classes, 5):
        print np.bincount(three_classes[train])
        
[  0  90 314 395] 
[  0  90 314 395]
[  0  90 314 395] 
[  0  91 315 395] 
[  0  91 315 396]

我们可以看到，我们得到了每个分类的样例大小，正好是训练集合测试集的比例。

5.5 菜鸟的网格搜索

这个秘籍中，我们打算使用 Python 来介绍基本的网格搜索，并且使用 Sklearn 来处理模型，以及 Matplotlib 来可视化。

准备

这个秘籍中，我们会执行下面这些东西：

在参数空间中设计基本的搜索网格。
迭代网格并检查数据集的参数空间中的每个点的损失或评分函数。
选取参数空阿基那种的点，它使评分函数最大或者最小。

同样，我们训练的模型是个基本的决策树分类器。我们的参数空间是 2 维的，有助于我们可视化。

1 2	criteria = {gini, entropy} max_features = {auto, log2, None}

参数空间是criteria和max_features的笛卡尔积。

我们会了解如何使用itertools来迭代这个空间。

让我们创建数据集来开始：

1 2	>>> from sklearn import datasets >>> X, y = datasets.make_classification(n_samples=2000, n_features=10)

操作步骤

之前我们说，我们使用网格搜索来调整两个参数 – criteria和max_features``criteria和max_features。我们需要将其表示为 Python 集合，之后使用itertools.product来迭代它们。

不错，所以既然我们拥有了参数空间，让我们迭代它并检查每个模型的准确率，它们由参数指定。之后，我们保存这个准确率，便于比较不同的参数空间。我们也会使用以50, 50划分的测试和训练集。

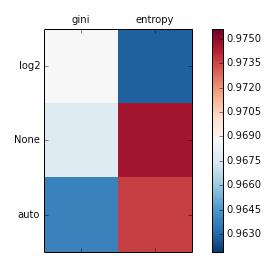
import numpy as np 
train_set = np.random.choice([True, False], size=len(y)) 
from sklearn.tree import DecisionTreeClassifier 
accuracies = {} 
for criterion, max_feature in parameter_space:
    dt = DecisionTreeClassifier(criterion=criterion,                
         max_features=max_feature)
    dt.fit(X[train_set], y[train_set])
    accuracies[(criterion, max_feature)] = (dt.predict(X[~train_set])
                                         == y[~train_set]).mean() 
>>> accuracies 
{('entropy', None): 0.974609375, ('entropy', 'auto'): 0.9736328125, ('entropy', 'log2'): 0.962890625, ('gini', None): 0.9677734375, ('gini', 'auto'): 0.9638671875, ('gini', 'log2'): 0.96875}

所以现在我们拥有了准确率和它的表现。让我们可视化它的表现。

>>> from matplotlib import pyplot as plt 
>>> from matplotlib import cm 
>>> cmap = cm.RdBu_r 
>>> f, ax = plt.subplots(figsize=(7, 4)) 
>>> ax.set_xticklabels([''] + list(criteria)) 
>>> ax.set_yticklabels([''] + list(max_features)) 
>>> plot_array = [] 
>>> for max_feature in max_features:
        m = [] 
>>> for criterion in criteria:       
        m.append(accuracies[(criterion, max_feature)])       
        plot_array.append(m) 
>>> colors = ax.matshow(plot_array, vmin=np.min(accuracies.values()) -
             0.001, vmax=np.max(accuracies.values()) + 0.001, cmap=cmap) 
>>> f.colorbar(colors)

输出如下：

很容易看到哪个表现最好。单元你可以使用爆破方式看到它如何进一步处理。

工作原理

原理很简单，我们只需要执行下列步骤：

选取一系列参数
迭代它们并求得每一步的准确率
通过可视化来寻找最佳的表现

5.6 爆破网格搜索

这个秘籍中，我们会使用 Sklearn 做一个详细的网格搜索。这基本和上一章的事情相同，但是我们使用内建方法。

我们也会浏览一个执行随机化优化的示例。这是个用于爆破搜索的替代方案。本质上，我们花费一些计算周期，来确保搜索了整个空间。我们在上一个秘籍中比较冷静，但是，你可以想想拥有多个步骤的模型，首先对缺失数据进行估算，之后使用 PCA 降低维度来分类。你的参数空间可能非常大，非常块，因此，搜索一部分空间是有利的。

准备

我们需要下列步骤来开始：

创建一些数据集
之后创建LogisticRegression 对象，训练我们的模型
之后，我们创建搜索对象，GridSearch 和RandomizedSearchCV

工作原理

执行下列代码来创建一些分类数据

1 2	>>> from sklearn.datasets import make_classification >>> X, y = make_classification(1000, n_features=5)

现在，我们创建逻辑回归对象：

1 2	>>> from sklearn.linear_model import LogisticRegression >>> lr = LogisticRegression(class_weight='auto')

我们需要指定打算搜索的参数。对于GridSearch，我们可以指定所关心的范围，但是对于RandomizedSearchCV，我们实际上需要指定相同空间上的分布：

>>> lr.fit(X, y)

LogisticRegression(C=1.0, class_weight={0: 0.25, 1: 0.75}, dual=False, 
                   fit_intercept=True, intercept_scaling=1,
                   penalty='l2', random_state=None, tol=0.0001)

>>> grid_search_params = {'penalty': ['l1', 'l2'],
                          'C': [1, 2, 3, 4]}

我们需要做的唯一一个修改，就是将C参数描述为概率分布。我们现在使其保持简单，虽然我们使用scipy来描述这个分布。

>>> import scipy.stats as st >>> import numpy as np
>>> random_search_params = {'penalty': ['l1', 'l2'],
                            'C': st.randint(1, 4)}

工作原理

现在，我们要训练分类器了。原理是将lr作为参数传给搜索对象。

1 2	>>> from sklearn.grid_search import GridSearchCV, RandomizedSearchCV >>> gs = GridSearchCV(lr, grid_search_params)

GridSearchCV 实现了和其他方法相同的 API：

>>> gs.fit(X, y)

GridSearchCV(cv=None, estimator=LogisticRegression(C=1.0,
            class_weight='auto', dual=False, fit_intercept=True,
            intercept_scaling=1, penalty='l2', random_state=None,
            tol=0.0001), fit_params={}, iid=True, loss_func=None,
            n_jobs=1, param_grid={'penalty': ['l1', 'l2'],
            'C': [1, 2, 3, 4]}, pre_dispatch='2*n_jobs', refit=True,
            score_func=None, scoring=None, verbose=0)

我们可以看到， param_grid参数中的penalty 和C都是数组。

为了评估得分，我们可以使用网格搜索的grid_scores_ 属性。我们也打算寻找参数的最优集合。我们也可以查看网格搜索的边际表现。

>>> gs.grid_scores_
[mean: 0.90300, std: 0.01192, params: {'penalty': 'l1', 'C': 1}, 
 mean: 0.90100, std: 0.01258, params: {'penalty': 'l2', 'C': 1}, 
 mean: 0.90200, std: 0.01117, params: {'penalty': 'l1', 'C': 2}, 
 mean: 0.90100, std: 0.01258, params: {'penalty': 'l2', 'C': 2}, 
 mean: 0.90200, std: 0.01117, params: {'penalty': 'l1', 'C': 3}, 
 mean: 0.90100, std: 0.01258, params: {'penalty': 'l2', 'C': 3}, 
 mean: 0.90100, std: 0.01258, params: {'penalty': 'l1', 'C': 4}, 
 mean: 0.90100, std: 0.01258, params: {'penalty': 'l2', 'C': 4}]

我们可能打算获取最大得分：

>>> gs.grid_scores_[1][1]
0.90100000000000002

>>> max(gs.grid_scores_, key=lambda x: x[1])
mean: 0.90300, std: 0.01192, params: {'penalty': 'l1', 'C': 1}

获取的参数就是我们的逻辑回归的最佳选择。

5.7 使用伪造的估计器来比较结果

这个秘籍关于创建伪造的估计其。这并不是一个漂亮或有趣的东西，但是我们值得为最后构建的模型创建一个参照点。

准备

这个秘籍中，我们会执行下列任务：

创建一些随机数据
训练多种伪造的估计器

我们会对回归数据和分类数据来执行这两个步骤。

操作步骤

首先，我们创建随机数据：

>>> X, y = make_regression()

>>> from sklearn import dummy

>>> dumdum = dummy.DummyRegressor()

>>> dumdum.fit(X, y)

DummyRegressor(constant=None, strategy='mean')

通常，估计器仅仅使用数据的均值来做预测。

1
2
3

>>> dumdum.predict(X)[:5]

array([ 2.23297907,  2.23297907,  2.23297907,  2.23297907,         2.23297907])

我们可以尝试另外两种策略。我们可以提供常数来做预测（就是上面命令中的constant=None），也可以使用中位值来预测。

如果策略是constant，才会使用提供的常数。

让我们看一看：

>>> predictors = [("mean", None),
                  ("median", None),
                  ("constant", 10)]
                  
>>> for strategy, constant in predictors:
        dumdum = dummy.DummyRegressor(strategy=strategy,
                 constant=constant) 

>>> dumdum.fit(X, y)    

>>> print "strategy: {}".format(strategy), ",".join(map(str,
          dumdum.predict(X)[:5]))
          
strategy: mean 2.23297906733,2.23297906733,2.23297906733,2.23297906733,2 .23297906733
strategy: median 20.38535248,20.38535248,20.38535248,20.38535248,20.38535 248 
strategy: constant 10.0,10.0,10.0,10.0,10.0

我们实际上有四种分类器的选项。这些策略类似于连续情况，但是适用于分类问题：

>>> predictors = [("constant", 0),
                  ("stratified", None),
                  ("uniform", None),
                  ("most_frequent", None)]

我们也需要创建一些分类数据：

>>> X, y = make_classification()
>>> for strategy, constant in predictors:
        dumdum = dummy.DummyClassifier(strategy=strategy,
                 constant=constant)
        dumdum.fit(X, y)
        print "strategy: {}".format(strategy), ",".join(map(str,
              dumdum.predict(X)[:5]))
strategy: constant 0,0,0,0,0 
strategy: stratified 1,0,0,1,0 
strategy: uniform 0,0,0,1,1 
strategy: most_frequent 1,1,1,1,1

工作原理

最好在最简单的模型上测试你的模型，这就是伪造的估计器的作用。例如，在一个模型中，5% 的数据是伪造的。所以，我们可能能够训练出一个漂亮的模型，而不需要猜测任何伪造。

我们可以通过使用分层（stratified）策略来床架买模型，使用下面的命令。我们也可以获取一个不错的示例，关于为什么分类的不均等会导致问题：

>>> X, y = make_classification(20000, weights=[.95, .05])

>>> dumdum = dummy.DummyClassifier(strategy='most_frequent')

>>> dumdum.fit(X, y)
DummyClassifier(constant=None, random_state=None, strategy='most_ frequent')

>>> from sklearn.metrics import accuracy_score

>>> print accuracy_score(y, dumdum.predict(X))

0.94575

我们实际上经常是正确的，但关键不是这个。关键是，这就是我们的基线。如果我们不能为伪造数据创建模型，并且比这个更准确，它就不值得我们花时间。

5.8 回归模型评估

我们已经学过了如何量化分类中的误差，现在我们讨论连续问题中的误差。例如，我们尝试预测年龄而不是性别。

准备

像分类一样，我们伪造一些数据，之后绘制变化。我们开始会很简单，之后逐步变复杂。数据是模拟的线性模型。

1
2
3

m = 2
b = 1
y = lambda x: m * x + b

同时，导入我们的模块：

1
2
3

>>> import numpy as np 
>>> import matplotlib.pyplot as plt 
>>> from sklearn import metrics

操作步骤

我们会执行下列操作：

使用y来生成y_actual
使用y_actual加上一些err生成y_prediction'
绘制差异
遍历不同的度量并绘制它们

让我们同时关注步骤 1 和 2，并且创建一个函数来帮助我们。这与我们刚刚看的相同，但是我们添加一些功能来指定误差（如果是个常量则为偏差）。

>>> def data(x, m=2, b=1, e=None, s=10):
        """         
        Args:           
            x: The x value           
            m: Slope           
            b: Intercept           
            e: Error, optional, True will give random error       
        """           
        
        if e is None:
            e_i = 0       
        elif e is True:
            e_i = np.random.normal(0, s, len(xs))
        else:
            e_i = e

        return x * m + b + e_i

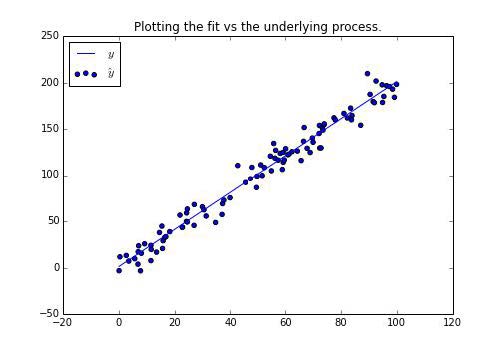
既然我们已经拥有了函数，让我们定义y_hat和y_actual。我们会以便利的方法来实现：

>>> from functools import partial

>>> N = 100 
>>> xs = np.sort(np.random.rand(N)*100)

>>> y_pred_gen = partial(data, x=xs, e=True) 
>>> y_true_gen = partial(data, x=xs)

>>> y_pred = y_pred_gen() 
>>> y_true = y_true_gen()

>>> f, ax = plt.subplots(figsize=(7, 5))

>>> ax.set_title("Plotting the fit vs the underlying process.") 
>>> ax.scatter(xs, y_pred, label=r'$\hat{y}$')

>>> ax.plot(xs, y_true, label=r'$y$')

>>> ax.legend(loc='best')

输出如下：

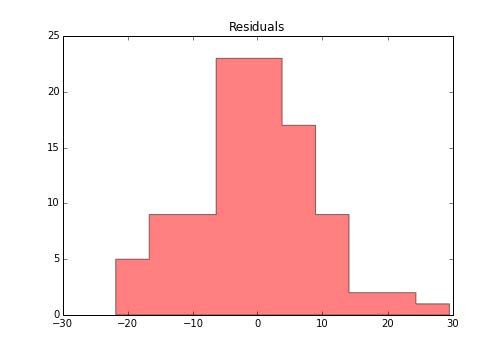
仅仅为了验证输出，我们要计算经典的残差。

>>> e_hat = y_pred - y_true

>>> f, ax = plt.subplots(figsize=(7, 5))

>>> ax.set_title("Residuals") 
>>> ax.hist(e_hat, color='r', alpha=.5, histtype='stepfilled')

输出如下：

看起来不错。

工作原理

现在让我们看看度量。

首先，一种度量就是均方误差。

1	MSE(y_trus, y_pred) = E((y_trus - y_pred)^2)

1	mse = ((y_trus - y_pred) ** 2).mean()

你可以使用下面的代码来计算均方误差值：

1
2
3

>>> metrics.mean_squared_error(y_true, y_pred)

93.342352628475368

要注意，这个代码会惩罚更大误差。要注意，我们这里所做的是，将模型的可能的损失函数应用于测试数据。

另一个萱萱个就是平均绝对差。我们需要计算差异的绝对值。如果我们不这么做，我们的值就可能接近于零，也就是分布的均值：

1	MAD(y_trus, y_pred) = E(\|y_trus - y_pred\|)

1	mad = np.abs(y_trus - y_pred).mean()

最终的选项是 R 平方，它是 1 减去拟合模型的均方误差，与整体均值的军方误差的比值。随着比值接近于 0，R 平方接近于 1。

1	rsq = 1 - ((y_trus - y_pred) 2).sum() / ((y_trus - y_trus.mean()) 2).sum()

1
2
3

>>> metrics.r2_score(y_true, y_pred)

0.9729312117010761

R 平方是描述性的，它不提供模型准确性的清晰感觉。

5.9 特征选取

这个秘籍以及后面那个都关于自动特征选取。我喜欢将其看做参数调整的特征替换。就像我们做交叉验证来寻找合适的通用参数，我们可以寻找合适的特征通用子集。这涉及到几种不同方式。

最简单的想法就是到那边了选取。其它方法涉及到处理特征的组合。

特征选取的一个额外好处就是，它可以减轻数据收集的负担。想象你已经在一个很小的数据子集上构建了模型。如果一切都很好，你可能打算扩展来预测数据的整个子集。如果是这样，你可以减少数据收集的工作量。

准备

在单变量选取中，评分函数又出现了。这次，它们会定义比较度量，我们可以用它来去掉一些特征。

这个秘籍中，我们会训练带有 10000 个特征的回归模型，但是只有 1000 个点。我们会浏览多种单变量特征选取方式。

1 2	>>> from sklearn import datasets >>> X, y = datasets.make_regression(1000, 10000)

既然我们拥有了数据，我们会使用多种方式来比较特征。当你进行文本分析，或者一些生物信息学分析时，这是个非常常见的情况。

操作步骤

首先，我们需要导入feature_selection模块。

1 2	>>> from sklearn import feature_selection >>> f, p = feature_selection.f_regression(X, y)

这里，f就是和每个线性模型的特征之一相关的 f 分数。我们之后可以比较这些特征，并基于这个比较，我们可以筛选特征。p是f值对应的 p 值。

在统计学中，p值是一个值的概率，它比检验统计量的当前值更极端。这里f值检验统计量。

>>> f[:5] 
array([  1.06271357e-03, 2.91136869e+00, 1.01886922e+00,
         2.22483130e+00, 4.67624756e-01]) 
>>> p[:5] 
array([ 0.97400066, 0.08826831, 0.31303204, 0.1361235, 0.49424067])

我们可以看到，许多p值都太大了。我们更想让p值变小。所以我们可以将 NumPy 从工具箱中取出来，并且选取小于.05的p值。这些就是我们用于分析的特征。

>>> import numpy as np 
>>> idx = np.arange(0, X.shape[1]) 
>>> features_to_keep = idx[p < .05] 
>>> len(features_to_keep)
501

你可以看到，我们实际上保留了相当大的特征总量。取决于模型的上下文，我们可以减少p至。这会减少保留的特征数量。

另一个选择是使用VarianceThreshold 对象。我们已经了解一些了。但是重要的是理解，我们训练模型的能力，基本上是基于特征所产生的变化。如果没有变化，我们的特征就不能描述独立变量的变化。根据文档，良好的特征可以用于非监督案例，因为它并不是结果变量。

我们需要设置起始值来筛选特征。为此，我们选取并提供特征方差的中位值。

>>> var_threshold = feature_selection.VarianceThreshold(np.median(np.
                    var(X, axis=1)))

>>> var_threshold.fit_transform(X).shape

(1000, 4835)

我们可以看到，我们筛选了几乎一半的特征，或多或少就是我们的预期。

工作原理

通常，所有这些方式的原理都是使用单个特征来训练基本的模型。取决于它是分类问题还是回归问题，我们可以使用合适的评分函数。

让我们观察一个更小的问题，并可视化特征选取如何筛选特定的特征。我们使用第一个示例的相同评分函数，但是仅仅有 20 个特征。

1
2
3

>>> X, y = datasets.make_regression(10000, 20)

>>> f, p = feature_selection.f_regression(X, y)

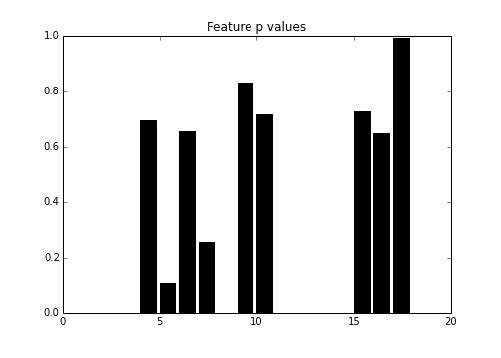
现在，让我们绘制特征的p值，我们可以看到筛选和保留哪个特征：

>>> from matplotlib import pyplot as plt

>>> f, ax = plt.subplots(figsize=(7, 5))

>>> ax.bar(np.arange(20), p, color='k') 
>>> ax.set_title("Feature p values")

输出如下：

我们可以看到，许多特征没有保留，但是保留了一些特征。

5.10 L1 范数上的特征选取

我们打算实现一些相似的理念，我们在套索回归的秘籍中见过他们。在那个米几种，我们查看了含有 0 系数的特征数量。

现在我们打算更进一步，并使用 L1 范数来预处理特征。

准备

我们要使用糖尿病数据集来拟合回归。首先，我们要使用ShuffleSplit 交叉验证来训练基本的LinearRegression 模型，之后，我们使用LassoRegression 来寻找 L1 惩罚为 0 的系数。我们希望它能帮助我们避免过拟合，也就是说这个模型非常特定于所训练的数据。换句话说，如果过拟合的话，模型并不能推广到外围的数据。

我们打算执行下列步骤：

加载数据集
训练基本的线性回归模型
使用特征选取来移除不提供信息的特征
重新训练线性回归，并与特征完整的模型相比，它拟合得多好。

操作步骤

首先加载数据集：

1 2	>>> import sklearn.datasets as ds >>> diabetes = ds.load_diabetes()

让我们导入度量模块的mean_squared_error函数，以及cross_validation模块的 ShuffleSplit交叉验证函数。

>>> from sklearn import metrics 
>>> from sklearn import cross_validation

>>> shuff = cross_validation.ShuffleSplit(diabetes.target.size

现在训练模型，我们会跟踪ShuffleSplit每次迭代中的均方误差。

>>> mses = [] 
>>> for train, test in shuff:
        train_X = diabetes.data[train]
        train_y = diabetes.target[train]
        
        test_X = diabetes.data[~train]
        test_y = diabetes.target[~train]
        
        lr.fit(train_X, train_y)   
        mses.append(metrics.mean_squared_error(test_y,               
                    lr.predict(test_X)))

>>> np.mean(mses)
2856.366626198198

所以既然我们做了常规拟合，让我们在筛选系数为 0 的特征之后再检查它。让我们训练套索回归：

>>> from sklearn import feature_selection 
>>> from sklearn import cross_validation

>>> cv = linear_model.LassoCV() 
>>> cv.fit(diabetes.data, diabetes.target) 
>>> cv.coef_

array([ -0. , -226.2375274 ,  526.85738059,  314.44026013,
        -196.92164002, 1.48742026, -151.78054083, 106.52846989,
        530.58541123, 64.50588257])

我们会移除第一个特征。我使用 NumPy 数组来表示模块中包含的列。

1
2
3

>>> import numpy as np 
>>> columns = np.arange(diabetes.data.shape[1])[cv.coef_ != 0] 
>>> columns array([1, 2, 3 4, 5, 6, 7, 8, 9])

好的，所以现在我们使用特定的特征来训练模型（请见下面代码中的列）：

>>> l1mses = []
>>> for train, test in shuff:
        train_X = diabetes.data[train][:, columns]
        train_y = diabetes.target[train]
        
        test_X = diabetes.data[~train][:, columns]
        test_y = diabetes.target[~train]
        
        lr.fit(train_X, train_y)           l1mses.append(metrics.mean_squared_error(test_y,            
                      lr.predict(test_X)))
                      
>>> np.mean(l1mses) 
2861.0763924492171 
>>> np.mean(l1mses) - np.mean(mses) 
4.7097662510191185

我们可以看到，即使我们移除了不提供信息的特征，模型依然不怎么样。这种情况不是始终发生。下一部分中，我们会比较模型间的拟合，其中有很多不提供信息的特征。

工作原理

首先，我们打算创建回归数据集，带有很多不提供信息的特征：

1	>>> X, y = ds.make_regression(noise=5)

让我们训练普通的回归：

>>> mses = []

>>> shuff = cross_validation.ShuffleSplit(y.size)

>>> for train, test in shuff:
        train_X = X[train]
        train_y = y[train]

        test_X = X[~train]
        test_y = y[~train]

        lr.fit(train_X, train_y)           mses.append(metrics.mean_squared_error(test_y,              
                    lr.predict(test_X))) 
                    
>>> np.mean(mses)
879.75447864034209

现在我们可以以相同个过程来使用套索回归：

>>> cv.fit(X, y)

LassoCV(alphas=None, copy_X=True, cv=None, eps=0.001,
        fit_intercept=True, max_iter=1000, n_alphas=100,
        n_jobs=1, normalize=False, positive=False, precompute='auto',
        tol=0.0001, verbose=False)

我们会再次创建列。这是个很好的模式，让我们能够制定要包含的列。

>>> import numpy as np 
>>> columns = np.arange(X.shape[1])[cv.coef_ != 0] 
>>> columns[:5] array([11, 15, 17, 20, 21,])
>>> mses = []

>>> shuff = cross_validation.ShuffleSplit(y.size)
>>> for train, test in shuff:
        train_X = X[train][:, columns]
        train_y = y[train]
        
        test_X = X[~train][:, columns]
        test_y = y[~train]
        
        lr.fit(train_X, train_y) 
        mses.append(metrics.mean_squared_error(test_y,              
                    lr.predict(test_X)))    
                    
>>> np.mean(mses)
15.755403220117708

我们可以看到，我们在模型的训练中获得了极大的提升。这刚好解释了，我们需要承认，不是所有特征都需要或者应该放进模型中。

5.11 使用 joblib 保存模型

这个秘籍中，我们打算展示如何保存模型，便于以后使用。例如，你可能打算实际使用模型来预测结果，并自动做出决策。

准备

这个秘籍中，我们会执行下列任务：

训练我们要保存的模型
导入 joblib 并保存模型

操作步骤

为了使用 joblib 保存我们的模型，可以使用下面的代码：

>>> from sklearn import datasets, tree
>>> X, y = datasets.make_classification()

>>> dt = tree.DecisionTreeClassifier() 
>>> dt.fit(X, y)

DecisionTreeClassifier(compute_importances=None, criterion='gini',
                       max_depth=None, max_features=None,
                       max_leaf_nodes=None, min_density=None,
                       min_samples_leaf=1, min_samples_split=2,
                       random_state=None, splitter='best')
                       
>>> from sklearn.externals import joblib
>>> joblib.dump(dt, "dtree.clf")
['dtree.clf', 
 'dtree.clf_01.npy',
 'dtree.clf_02.npy',
 'dtree.clf_03.npy',
 'dtree.clf_04.npy']

工作原理

上面的下面的原理是，保存对象状态，可以重新加载进 Sklearn 对象。要注意，对于不同的模型类型，模型的状态拥有不同的复杂度级别。

出于简单的因素，将我们要保存的东西看做一种方式，我们提供出入来预测结果。对于回归来说很简单，简单的线性代数就足以。但是，对于像是随机森林的模型，我们可能拥有很多颗树。这些树可能拥有不同的复杂度级别，比较困难。

我们可以简单随机森林模型的大小：

>>> from sklearn import ensemble

>>> rf = ensemble.RandomForestClassifier() 
>>> rf.fit(X, y)

RandomForestClassifier(bootstrap=True, compute_importances=None,
                        criterion='gini', max_depth=None,
                        max_features='auto', max_leaf_nodes=None,
                        min_density=None, min_samples_leaf=1,
                        min_samples_split=2, n_estimators=10,
                        n_jobs=1, oob_score=False,
                        random_state=None, verbose=0)

我打算省略输出，但是总之，我的机器上一共有 52 个输出文件。

>>> joblib.dump(rf, "rf.clf") 
['rf.clf', 
 'rf.clf_01.npy', 
 'rf.clf_02.npy', 
 'rf.clf_03.npy', 
 'rf.clf_04.npy', 
 'rf.clf_05.npy', 
 'rf.clf_06.npy',
 ...             ]

第五章 模型后处理

5.1 K-fold 交叉验证

准备

工作原理

工作原理

5.2 自动化交叉验证

准备

工作原理

工作原理

5.3 使用 ShuffleSplit 交叉验证

准备

操作步骤

5.4 分层的 k-fold

准备

操作步骤

工作原理

5.5 菜鸟的网格搜索

准备

操作步骤

工作原理

5.6 爆破网格搜索

准备

工作原理

工作原理

5.7 使用伪造的估计器来比较结果

准备

操作步骤

工作原理

5.8 回归模型评估

准备

操作步骤

工作原理

5.9 特征选取

准备

操作步骤

工作原理

5.10 L1 范数上的特征选取

准备

操作步骤

工作原理

5.11 使用 joblib 保存模型

准备

操作步骤

工作原理

更多

第五章模型后处理